shabrina: 2011

Kamis, 24 Maret 2011

usaha dan energi FISIKA

A. Bentuk Energi dan Perubahannya
1. Energi (disebut juga tenaga) adalah kemampuan untuk melakukan usaha.
2. Bentuk-Bentuk Energi
a) Energi Mekanik

Benda yang bergerak atau memiliki kemampuan untuk bergerak, memiliki energi mekanik. Air terjun yang berada di puncak tebing memiliki energi mekanik yang cukup besar, demikian juga dengan angin.
b) Energi Bunyi
Energi bunyi adalaj energi yang dihasilkan oleh getaran partikel-partikel udara disekitar sebuah sumber bunyi. Contoh : Ketika radio atau televisi beroperasi, pengeras suara secara nyata menggerakkan udara didepannya. Caranya dengan menyebabkan partikel-partikel udara itu bergetar. Energi dari getaran partikel-partikel udara ini sampai ditelinga, sehingga kamu dapat mendengar.
c) Energi kalor
Energi kalor adalah energi yang dihasilkan oleh gerak internal partikel-partikel dalam suatu zat. Contoh : apabila kedua tanganmu digosok-gosokkan selam beberapa detik maka tanganmu akan terasa panas. Umumnya energi kalor dihasilkan dari gesekan. Energi kalor menyebabkan perubahan suhu dan perubahan wujud.
d) Energi Cahaya
Energi Cahaya adalah energi yang dihasilkan oleh radiasi gelombang elektromagnetik
e) Energi Listrik
Energi Listrik adalah energi yang dihasilkan oleh muatan listrik yang bergerak melalui kabel.
f) Energi Nuklir
Energi nuklir adalah energi yang dihasilkan oleh reaksi inti dari bahan radioaktif. Ada dua jenis energi nuklir yaitu energi nuklir fisi dan fusi. Energi nuklir fisi terjadi pada reaktor atom PLTN. Ketika suatu inti berat (misal uranium) membelah (fisi), energi nuklir cukup besar dibebaskan dalam bentuk energi kalor dan energi cahaya. Energi nuklir juga dibebaskan ketika inti-inti ringan (misalnya hidrogen) bertumbukan pada kelajuan tinggi dan bergabung (fusi). Energi matahari dihasilkan dari suatu reaksi niklir fusi dimana inti-inti hidrogen bergabung membentuk inti helium.

3. Energi Mekanik
Energi mekanik adalah energi yang berkaitan dengan gerak atau kemampuan untuk bergerak. Ada dua macam energi mekanik yaitu ; energi kinetik dan energi potensial.
a. Energi kinetik
Energi kinetik adalah energi yang dimiliki benda karena geraknya atau kelajuannya. Energi kinetik dirumuskan :

EK = energi kinetik (joule atau J), m = massa (kg), v = kelajuan
b. Energi Potensial
Energi potensial adalah energi yang dimiliki oleh benda karena posisinya. Energi potensial dapat dirumuskan:

EP = energi potensial gravitasi (joule atau J), m = massa (kg), g = percepatan gravitasi (m/s2), h = ketinggian benda dari acuan (m).

4. Konsep Energi dan Perubahannya dalam keseharian
a. Konversi energi
Konversi energi adalah perubahan bentuk energi dari bentuk satu ke bentuk lainnya. Contoh

b. Konverter energi
Konverter energi adalah alat atau benda yang melakukan konversi energi. Beberapa konverter energi yaitu:
1. Setrika listrik mengubah energi listrik menjadi kalor
2. Ayunan mengubah energi kinetik menjadi energi potensial …energi potensial menjadi energi kinetik
3. Rem mobil mengubah energi kinetik menjadi energi kalor.

5. Hukum Kekekalan Energi berbunyi energi tidak dapat diciptakan dan tidak dapat dimusnahkan, energi hanya dapat diubah dari satu bentuk ke bentuk yang lainnya.
6. Sumber-Sumber Energi dibagi menjadi beberapa kelompok yaitu:
a) Sumber energi yang dapat diperbarui dan tak dapat diperbarui.
• Contoh sumber energi yang dapat diperbaharui adalah air, angin, dan surya. Dikatakan sumber energi ini dapat diperbahrui karena sumber energi ini persediaanya sangat melimpah di bumi dan kita dapat menggunakannya terus-menerus tanpa khawatir akan habis.
• Contoh sumber energi yang tidak dapat diperbaharui adalah minyak, gas, batu bara. Dikatakan sumber energi ini tidak dapat diperbahrui karena sumber energi ini persediaannya terbatas di bumi dan sekali habis maka sumber ini tidak dapat digantikan atau diperbaharui. Oleh klarena itu kita harus bijaksana dalam menggunakannya.
b) Energi Konvensional
Energi konvensional : minyak, gas dan batu bara disebut juga energi fosil karena ketiga energi ini berasal dari bangkai-bangkai organisme dan tumbuh-tumbuhan yang tertimbun selama ratusan juta tahun yang lalu, serta tidak dapat diperbarui. Contoh : bahan bakar minyak (BBM), gas alam.
c) Berbagai energi alternatif dari sumber energi terbarui
1 Energi angin
Kincir angin sekarang digunakan untuk memutar generator listrik sehingga menghasilkan tenaga listrik.

2 Energi air
Air yang memiliki energi potensial tertentu dibendung pada suatu tempat. Air yang jatuh disalurkan melalui pipa pesat untuk diarahkan ke sudu-sudu turbin air sehingga energi kinetik air dapat dimanfaatkan untuk menggerakkan turbin. Turbin dihubungkan dengan generator melalui satu poros, sehingga generator akan berpytar dan menghasilkan listrik. Karena diperlukan kelajuan air tertentu pada aliran sungai, hanya sedikit tempat didunia yang memenuhi syarat untuk dibangun PLTA.
3 Energi panas bumi
Batuan panas terbentuk beberapa kilometer dibawah permukaan bumi memanaskan air disekitarnya sehingga akan menghasilkan sumber uap panas atau geiser. Sumber panas bumi ini dibor. Uap panas yang keluar dari pengeboran setelah disaring digunakan untuk menggerakkan generator sehingga menghasilkan energi listrik. Contoh : Pusat Listrik Tenaga Panas Bumi (PLTP), yang telah beroperasi PLTP Kamojang Jawa Barat.

B. Konsep Usaha dan Energi
Dalam fisika usaha yang dilakukan oleh sebuah gaya didefinisikan sebagai hasil kali gaya dengan perpindahan benda yang searah dengan gaya. Dapat dirumuskan :

Satuan usaha dalam SI adalah joule. Satu joule adalah besar usaha yang dilakukan oleh gaya satu newton untuk memindahkan suatu benda searah gaya sejauh satu meter.
Kaitan usaha dan energi yaitu besar usaha yang dilakukan oleh suatu gaya dalam proses apa saja adalah sama dengan besar energi yang dipindahkan.

Usaha oleh Beberapa Gaya
Apabila usaha yang dilakukan oleh orang pertama dan orang kedua untuk memindahkan suatu benda ke kanan sejauh s adalah
W1 = F1 s (*) dan W2 = F2 s (**)
Telah diketahui bahwa resultan dua gaya searah adalah F =F1 + F2, sehingga usaha total yang dilakukan oleh kedua benda tersebut adalah
W = F s, W = (F1 + F2) s
Dengan memasukkan F1 s = W1 (lihat *) dan F2 s =W2 (lihat **), maka diperoleh
W = W1 + W2
Secara umum dapat disimpulkan sebagai berikut :
”Usaha ynag dilakukan oleh resultan gaya-gaya searah dan berlawanan arah, yang menyebabkan benda berpindah sejauh s, sama dengan jumlah usaha oleh tiap-tiap gaya”

C. DAYA

Daya didefinisikan sebagai usaha yang dilakukan gaya dalam satu satuan waktu. Karena tiap besaran yang dibagi dengan selang waktu disebut sebagai laju, daya juga didefinisikan sebagai laju melakukan usaha. Karena usaha selalu muncul apabila terjadi perubahan bentuk energi. Daya juga dapat didefinisikan sebagai laju perubahan energi dari satu bentuk ke bentuk lainnya. Daya dirumuskan sebagai

Dengan P = daya (watt), W = usaha (joule), t = selang waktu (sekon).

D. PESAWAT SEDERHANA
Setiap alat yang mempermudah kita melakukan usaha disebut pesawat atau mesin. Pada dasarnya , ada empat macam pesawat sederhana yaitu tuas, katrol, bidang miring dan roda gigi.
a. Tuas
Tuas adalah pesawat sederhana yang berbentuk batang keras sempti yang dapat berputar disekitar satu titik. Titik ini disebut titik tumpu. Contoh tuas yang banyak dikenal adalah linggis. Linggis berbentuk satu batang besi (atau baja) yang digunakan untuk memudahkan menggeser suatu benda berat yang secara langsung sukar digeser oleh gaya otot manusia.
Perbandingan antara beban yang diangkat dan kuasa yang dilakukan disebut keuntungan mekanis. Keuntungan mekanis dirumuskan :

b. Katrol
Katrol adalah mesin sederhana yang terdiri dari sebuah roda beralur dimana seutas tali atau rantai dapat bergerak ulang-alik. Macam-macam katrol:
• Katrol tunggal tetap. Berfungsi mengubah arah gaya tarik dari menarik ke atas menjadi ke bawah. Contoh : ketika kita menaikkan bendera ke puncak maka dengan mudah bendera itu naik karena ada sebuah katrol tunggal tetap yang terpasang pada puncak tiang.
• Katrol tunggal bergerak. Katrol tunggal bergerak berfungsi memperbesar gaya.

c. Bidang Miring
Bidang miring adalah suatu permukaan miring yang penampangnya berbentuk segitiga. Contoh bidang miring yaitu tangga rumah berbentuk spiral.

d. Roda Gigi
Roda gigi atau gir adalah sepasang roda bergigi saling bersambungan yang dapat digunakan untuk menambah atau mengurangi gaya, disamping untuk mengubah besar dan arah kecepatan putaran.
7 Okt 2008 … Pokok bahasan Usaha dan Energi yang telah anda pelajari di SMP masih … Pahamilah dengan baik dan benar konsep Usaha dan Energi yang …

Usaha Dan energi

was posted on Monday, September 7th, 2009 at 5:46 amand is filed under Video.

titik berat (tugas fisika)

Dimanakah titik beratnya ?

Misalkan titik beratnya (x,y), nyatakan x dan y dalam a,b, dan t.

haha, berhubung saya paham tentang ini, jadi sini saya coba jelasin

misal kita ambil bangun ruang segitiga yang dibentuk oleh titik (0,0) (0,4) dan (4,4)
gambarnya kayak gini:

berarti persamaan garisnya bisa kita ambil y= x dari 0 sampe 4
kemudian garis tengahnya ada di
$y=\frac x2$
bisa dibilang didapet dari rata-ratanya kedua pembatas yaitu (kurva atas(y=x) dan kurva bawah(y=0) bagi 2)
nah kemudian, tau cara nyari titik pusat kotak yang dideret-deret kan
$y_{pusat} = \frac{(y_{pusat1}*luas1)+(y_{pusat2}*Luas2)+(y_{pusat3}*luas3)...}{luas1+Luas2+luas3}$
nah, dengan cara yang sama.
tapi kalo untuk mencari titik pusat, kita mempartisi segitiga ini menjadi bagian yang sangat kecil(lebarnya mendekati 0,tapi panjangnya sama dengan jarak antara kedua kurva)
$y_{pusat} = \frac{{\int_0^4 \frac x2*x dx}}{\int_0^4 x dx}$
note: x/2 menyatakan tempat titik tengahnya untuk tiap x;
sementara x me~~nyatakan~~ representasikan luasannya (bisa dibilang begitu)
$y_{pusat} = \frac {\frac{32}3}{8}$
$y_{pusat} = 4/3$
tepat seperti yang kita harapkan kan?

dengan cara yang sama, kalo nyari Xpusat, maka kita mempartisinya kearah y, dan selanjutnya lakukan hal yang sama
dapetnya hmm...
mboh'e males nyari, cobain aja ^^

ntar kalo udah bisa coba cari titik pusat luasan diantara 2 kurva (y=x^2) dan y=0 ^^
CMIIW

tugas fisika bab keseimbangan benda tegar

Keseimbangan Benda Tegar : Titik Berat

Telah dikatakan sebelumnya bahwa suatu benda tegar dapat mengalami gerak translasi (gerak lurus) dan gerak rotasi. Benda tegar akan melakukan gerak translasi apabila gaya yang diberikan pada benda tepat mengenai suatu titik yang yang disebut titik berat.

Benda akan seimbang jika pas diletakkan di titik beratnya

Titik berat merupakan titik dimana benda akan berada dalam keseimbangan rotasi (tidak mengalami rotasi). Pada saat benda tegar mengalami gerak translasi dan rotasi sekaligus, maka pada saat itu titik berat akan bertindak sebagai sumbu rotasi dan lintasan gerak dari titik berat ini menggambarkan lintasan gerak translasinya.

Mari kita tinjau suatu benda tegar, misalnya tongkat pemukul kasti, kemudian kita lempar sambil sedikit berputar. Kalau kita perhatikan secara aeksama, gerakan tongkat pemukul tadi dapat kita gambarkan seperti membentuk suatu lintasan dari gerak translasi yang sedang dijalani dimana pada kasus ini lintasannya berbentuk parabola. Tongkat ini memang berputar pada porosnya, yaitu tepat di titik beratnya. Dan, secara keseluruhan benda bergerak dalam lintasan parabola. Lintasan ini merupakan lintasan dari posisi titik berat benda tersebut.

Demikian halnya seorang peloncat indah yang sedang terjun ke kolam renang. Dia melakukan gerak berputar saat terjun. sebagaimana tongkat pada contoh di atas, peloncat indah itu juga menjalani gerak parabola yang bisa dilihat dari lintasan titik beratnya. Perhatikan gambar berikut ini.

seorang yang meloncat ke air dengan berputar

Jadi, lintasan gerak translasi dari benda tegar dapat ditinjau sebagai lintasan dari letak titik berat benda tersebut. Dari peristiwa ini tampak bahwa peranan titik berat begitu penting dalam menggambarkangerak benda tegar.

Cara untuk mengetahui letak titik berat suatu benda tegar akan menjadi mudah untuk benda-benda yang memiliki simetri tertentu, misalnya segitiga, kubus, balok, bujur sangkar, bola dan lain-lain. Yaitu d sama dengan letak sumbu simetrinya. Hal ini jelas terlihat pada contoh diatas bahwa letak titik berat sama dengan sumbu rotasi yang tidak lain adalah sumbu simetrinya.

Orang ini berada dalam keseimbangan

Di sisi lain untuk benda-benda yang mempunyai bentuk sembarang letak titik berat dicari dengan perhitungan. Perhitungan didasarkan pada asumsi bahwa kita dapat mengambil beberapa titik dari benda yang ingin dihitung titik beratnya dikalikan dengan berat di masing-masing titik kemudian dijumlahkan dan dibagi dengan jumlah berat pada tiap-tiap titik. dikatakan titik berat juga merupakan pusat massa di dekat permukaan bumi, namun untuk tempat yang ketinggiannya tertentu di atas bumi titik berat dan pusat massa harus dibedakan.

tugas fisika bab keseimbangan partikel

Suatu partikel disebut dalam keadaan seimbang, bila jumlah aljabar gaya-gaya yang bekerja pada partikel tersebut nol.
Syarat keseimbangan partikel adalah : F = 0
Jika partikel terletak pada bidang XY maka syarat keseimbangan : FX = 0 dan FY = 0

tugas fisika bab momen inersia

MOMEN INERSIA

Momen inersia (Satuan SI : kg m²) adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi daripada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.
Lambang

I

dan kadang-kadang juga

J

biasanya digunakan untuk merujuk kepada momen inersia.
Konsep ini diperkenalkan oleh Euler dalam bukunya a Theoria motus corporum solidorum seu rigidorum pada tahun 1730. Dalam buku tersebut, dia mengupas momen inersia dan banyak konsep terkait.

Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:

$I = \int r^2 \,dm\,\!$

di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.

Analisis

Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh

$I \triangleq m r^2\,\!$

Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik m_i dengan jarak r_i terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:

$I \triangleq \sum_{i=1}^{N} {m_{i} r_{i}^2}\,\!$

Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:

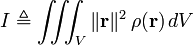
$I \triangleq \iiint_V \|\mathbf{r}\|^2 \,\rho(\mathbf{r})\,dV \!$

di mana

V adalah volume yang ditempati objek

ρ adalah fungsi kerapatan spasial objek

r = (r,θ,φ), (x,y,z), atau (r,θ,z) adalah vektor (tegaklurus terhadap sumbu rotasi) antara sumbu rotasi dan titik di benda tersebut.

Diagram perhitungan momen inersia sebuah piringan. Di sini k adalah 1/2 dan $\mathbf{r}$ adalah jari-jari yang digunakan untuk menentukan momen inersia

Berdasarkan analisis dimensi saja, momen inersia sebuah objek bukan titik haruslah mengambil bentuk:

$I = k\cdot M\cdot {R}^2 \,\!$

di mana

M adalah massa

R adalah jari-jari objek dari pusat massa (dalam beberapa kasus, panjang objek yang digunakan)

k adalah konstanta tidak berdimensi yang dinamakan "konstanta inersia", yang berbeda-beda tergantung pada objek terkait.

Konstanta inersia digunakan untuk memperhitungkan perbedaan letak massa dari pusat rotasi. Contoh:

k = 1, cincin tipis atau silinder tipis di sekeliling pusat
k = 2/5, bola pejal di sekitar pusat
k = 1/2, silinder atau piringan pejal di sekitar pusat.

tugas fisika bab momentum

Dalam mekanika klasik, momentum (dilambangkan dengan P) didefinisikan sebagai hasil perkalian dari massa dan kecepatan, sehingga menghasilkan vektor.
Momentum suatu benda (P) yang bermassa m dan bergerak dengan kecepatan v didefinisikan sebagai ::

$\mathbf{P}= m \mathbf{v}\,\!$

Massa merupakan besaran skalar, sedangkan kecepatan merupakan besaran vektor. Perkalian antara besaran skalar dengan besaran vektor akan menghasilkan besaran vektor. Jadi, momentum merupakan besaran vektor. Momentum sebuah partikel dapat dipandang sebagai ukuran kesulitan untuk mendiamkan benda. Sebagai contoh, sebuah truk berat mempunyai momentum yang lebih besar dibandingkan mobil yang ringan yang bergerak dengan kelajuan yang sama. Gaya yang lebih besar dibutuhkan untuk menghentikan truk tersebut dibandingkan dengan mobil yang ringan dalam waktu tertentu. (Besaran mv kadang-kadang dinyatakan sebagai momentum linier partikel untuk membedakannya dari momentum angular).

Hukum Kekekalan Momentum

Sama seperti energi, dalam kondisi tertentu, momentum suatu sistem akan kekal atau tidak berubah. Untuk memberikan pemahaman mengenai hal tersebut, maka akan digunakan konsep Pusat Massa. Misal jika ada sebuah sistem yang terdiri dari beberapa benda dengan massa $\mathbf{m_1}, \mathbf{m_2}, \mathbf{.....}.$ bergerak dengan kecepatan masing-masing adalah $\mathbf{v_1}, \mathbf{v_2}, \mathbf{.....}.$ , maka kecepatan pusat massa sistem tersebut adalah :

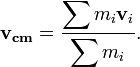
$\mathbf{v_{cm}} = { \displaystyle\sum m_i \mathbf{v}_i \over \displaystyle\sum m_i }.$

Dan jika sistem tersebut bergerak dengan dipercepat dengan percepatan masing-masing adalah $\mathbf{a_1}, \mathbf{a_2}, \mathbf{.....}.$ , maka percepatan pusat massa sistem tersebut adalah :

$\mathbf{a_{cm}} = { \displaystyle\sum m_i \mathbf{a}_i \over \displaystyle\sum m_i }.$

Sekarang jika benda-benda tersebut masing-masing diberi gaya $\mathbf{F_1}, \mathbf{F_2}, \mathbf{.....}.$ , maka benda-benda tersebut masing-masing memiliki percepatan :

$\mathbf{a_{i}} = { \mathbf{F_i} \over m_i }.$

Sehingga percepatan pusat massa sistem dapat dinyatakan sebagai :

$\mathbf{a_{cm}} = { \displaystyle\sum \mathbf{F}_i \over \displaystyle\sum m_i }.$

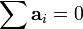Notasi $\displaystyle\sum \mathbf{F}_i.$ merupakan notasi yang menyatakan resultan gaya yang bekerja pada sistem tersebut. Jika resultan gaya yang bekerja pada sistem bernilai nol ( $\displaystyle\sum \mathbf{F}_i = 0$ ), maka sistem tersebut tidak dipercepat ( $\displaystyle\sum \mathbf{a}_i = 0$ ). Jika sistem tidak dipercepat, artinya sistem tersebut kecepatan pusat massa sistem tersebut konstan ( 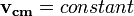$\mathbf{v_{cm}} = constant$ ). Jadi dapat disimpulkan bahwa :

$\displaystyle\sum m_i \mathbf{v}_i = constant.$

Notasi di atas merupakan notasi dari hukum kekekalan momentum. Jadi total momentum suatu sistem akan selalu kekal hanya jika resultan gaya yang bekerja pada sistem tersebut bernilai nol.